Abstract
The main objective of this paper is to give a wide study on the conformable fractional Legendre polynomials (CFLPs). This study is assumed to be a generalization
and refinement, in an easy way, of the scalar case into the context of the conformable
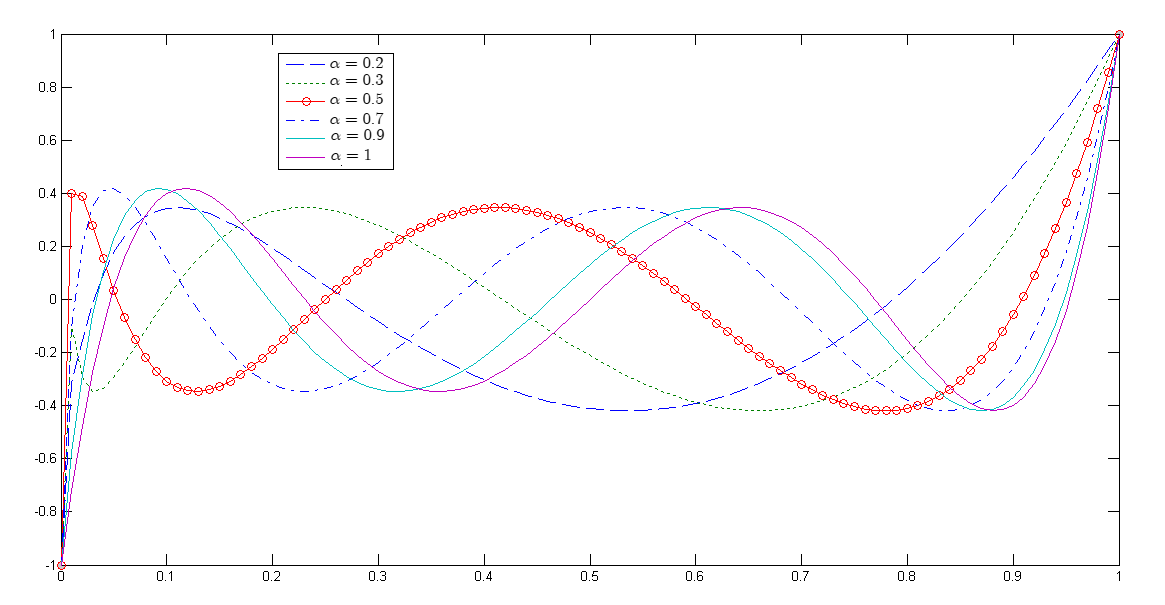
fractional differentiation. We introduce the CFLPs via different generating functions
and provide some of their main properties and convergence results. Subsequently,
some pure recurrence and differential recurrence relations, Laplace’s first integral formula and orthogonal properties are then developed for CFLPs. We append our study
with presenting shifted CFLPs and describing applicable scheme using the collocation method to solve some fractional differential equations (FDEs) in the sense of
conformable derivative. Some useful examples of FDEs are treated to support our theoretical results and examining their exact solutions. To the best of our knowledge, the
obtained results are newly presented and could enrich the fractional theory of special
functions.